Coupled Genetic Algorithm-Neural Network Model Kosi
Coupled Genetic Algorithm-Neural Network Model for Forecasting Monsoon Floods in Kosi River at Baltara (India)
Mani Kumar, PhD Scholar, B. I. T. Patna, e-mail: mani1794@yahoo.co.in
Rajeev R Sahay, Professor, B. I. T. Patna, e-mail: Rajeev_sahay@yahoo.com
ABSTRACT
A coupled model, GANN is developed embedding genetic algorithm (GA) and artificial neural network (ANN) for forecasting 1-day-ahead floods in the Kosi River in India for the monsoon season (June to October). The Kosi carries large flows during monsoon, making the entire North Bihar State of India unsafe for habitation or cultivation. When compared, GANN models are found simulating river flows better than autoregression models (ARs) developed for comparison purpose. The best performing GANN model, with four previous days’ flow-rates as inputs, predicts monsoon flows in the Kosi with the highest accuracy of 99.2%, the minimum root mean square errors of 83.1 m3/s and the maximum coefficient of correlation of 0.99.
KEYWORD: ANN, Flood Forecasting, Genetic Algorithm, Kosi, North Bihar, India
INTRODUCTION
The monsoon floods are a recurring hazard in most countries of South-East Asia. Year after year the monsoon deluge poses a challenge to the affected Community. According to the World Disasters Report 2006, about 58% of the total number of people killed due to natural disasters, mainly monsoon floods, during 1996-2005 was from India, Bangladesh and Indonesia. In coming years, North Asia and South-East Asia in particular are expected to experience extreme rainfall and greater flooding due to global warming. We are well aware that floods cannot be completely avoided, yet the severity of floods can be minimized if their occurrence is foretold. A reliable flood forecasting model can go a long way in reducing the impact of floods on human life, health and property especially in a densely populated basin like Kosi in India.
Many methods and models developed for river flow prediction in recent years can broadly be kept into two categories, concept-based and data-based. The concept-based models are unpopular as they require large data and complicated differential equations for their implementation. Moreover, difficulty arises in calibrating and testing these conceptual models with a single observation such as stream flow at a gauge-site, as is the case in this study. Data-based models, on the other hand, which are essentially based on statistical or artificial intelligence, have become popular in hydrological applications due to their simplicity, rapid development time and fewer data requirement. However, statistical models are found unsuitable for their difficulty in handling data with transitory characteristics such as drifts, trends and abrupt changes. On comparison, models based on artificial intelligence have the capability of learning the fluctuating relationship between input and output datasets without going into the knowledge of the physical processes occurring within the system. Artificial neural network is by far the most widely used artificial intelligence model. The ability of ANNs to capture relationships from given patterns has enabled them to be employed in various hydraulic and hydrologic problems such as modelling of river runoff (Minns and Hall 1996; Hsu et al. 1995; Smith and Eli 1995; Nagesh et al. 2002), stream water level (Thirumalaiah and Deo 1998; Randal et al. 2002; Jothiprakash et al. 2011, Taormina et al. 2012), river salinity (Maier and Dandy 1996), river flow (Karunanithi et al. 1994; Ozgur 2004; Jeevaragagam and Simonovic 2012), evapotranspiration (Trajkovic et al. 2003), ground water table fluctuation (Shukla et al. 1996; Yang et al.1996), reservoir operation rule (Chakraborty et al. 1992; Jain et al. 1999; Cancelliere et al. 2002), to name a few.
GA-Optimized Artificial Neural Networks (GANN)
GANN is a hybrid integration of GA and ANN. ANN, inspired by biological nervous systems, are composed of interconnected elements called neurons with a unique capability of recognizing underlying relationships between input and output events. For this, there has been an increasing trend in recent years towards the use of ANNs for water related research and engineering projects, and in particular, for modelling hydrological processes. A critical review of the concepts and applications of ANN in the field of hydrology can be found in ASCE (2000a, b).
Although ANN is a flexible and powerful mapping tool, initialization of weights and biases has a significant effect on network performance. We have taken the help of genetic algorithm to search for the optimal initial values of the selected ANN. The working of GA can be found in the books of Michalewicz (1992), Goldberg (2001) or Deb (2002). A hybrid integration of these two algorithms may take advantage of the characteristics of both schemes. It can increase solution stability and improve the performance of an ANN model, though at the expense of computational time. Hence, in a genetic algorithm-artificial neural network model i.e., GANN, initial parameters of the network are first optimized by GA prior to training by the conventional NN. The GA scheme, in our study, is implemented using GA Toolbox of MATLAB 7 and the binary code of representation is adopted for the variables of a selected ANN structure. A string length of 10 is used to represent each variable. This string length is sufficient for the range of values these variables can attain. The working structure of GANN model is shown in Figure 1.
Figure 1: Working structure of GANN model
MODEL IMPLEMENTATION
Developed models are evaluated for predicting 1-day-ahead flows in the Kosi at Baltara (India). The Kosi rises in the Great Himalayan Range of Nepal and Tibet at an altitude of over 7000 m. The Mount Everest, the highest peak in the world, lies in the catchment of the Kosi, which has a catchment area of approximately 69100 km2 out of which 29300 km2 lies in Tibet, 30600 km2 lies in Nepal and 9200 km2 lies in India. The alluvial fan of the Kosi is one of the largest in the world, extending from Barahksetra in Nepal to the Indo-Gangetic Plain of North Bihar of India. Its basin is surrounded by the ridges separating it from the Brahmaputra in the north, the Gandaki in the west, the Mahananda in the east and the Ganga in the south. The Kamla, the Baghmati (Kareh) and the Budhi Gandak are major tributaries of the Kosi in India, besides minor tributaries like Bhutahi Balan. The catchment map of the Kosi along with its adjoining rivers is shown in Figure 2.
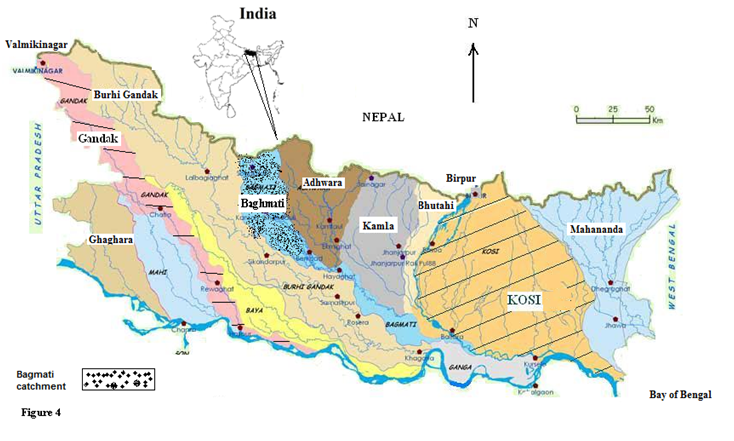
Figure 2: Catchment map of North Bihar (India) Rivers (fmis 2012)
For deriving the models, 357 daily monsoon flow rates for the year 2005-07 were utilized, while another 235 daily flows for the monsoon period for the year 2008-9 were utilized for verifying them. Table 1 summarizes the statistical information on the observed datasets for the Kosi River at Baltara Gauge Site.
Table 1. Statistical parameters for the Kosi River at Baltara
| Parameter | Derivation dataset | Verification dataset |
| Min. daily disch. (m3/s) | 1,660.0 | 1,240.0 |
| Meandaily disch. (m3/s) | 5,077.9 | 3,107.7 |
| Std. Dev. (m3/s) | 1596.17 | 849.07 |
| Range (m3/s) | 5,605.0 | 3,320.0 |
In addition to GANN class of models, another class of models, i.e. auto-regression class of models, are also developed for the purpose of performance comparison. Based on different inputs, four models in each class of models, i.e., GANN1, GANN2, GANN3 and GANN4 in GANN class and AR1, AR2, AR3 and AR4 in AR class are developed. For example, GANN3 and AR3 have three days’ antecedent flows from the observed flow time series, i.e., Qt, Qt-1 and Qt-2, for input (Table 2). The desired output in all models is 1-day-ahead flow, i.e., Qt+1. To allow performance comparison among the models, the following statistical indices are used:
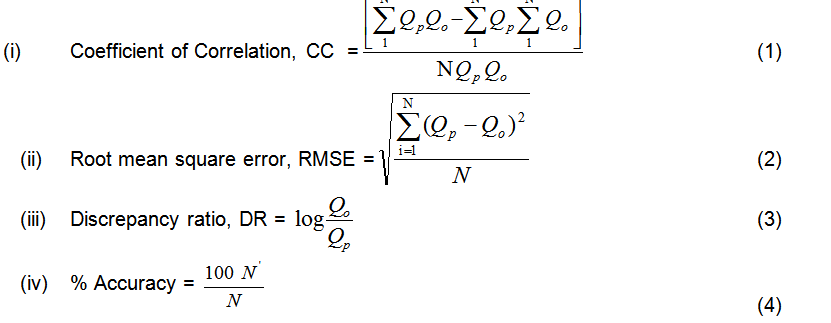
where
and 
are the predicted and the observed daily flow rates in the river respectively; N is the number of observations and is the number of the predicted values lying between 75% and 125% of the observed values (i.e., DR value of the prediction lying between -0.097 and 0.097). From Eq. (7), DR=0 suggests exact matching between the observed and predicted values, otherwise, there is either over prediction [DR>0, i.e.>] or under prediction [DR<0, i.e. <].
Table 2. Performance indices of models for Kosi River at Baltara (India)
Set/Input variables |
Model |
Derivation |
Verification |
Complete dataset |
||||||
CC |
RMSE |
CC |
RMSE |
CC |
RMSE |
DR Range |
Accuracy |
|||
Set 1 |
Qt |
AR1 |
0.994 |
174.3 |
0.988 |
140.6 |
0.995 |
158.0 |
-0.13 to 0.12 |
96.3 |
GANN1 |
0.994 |
170.8 |
0.988 |
128.8 |
0.995 |
151.3 |
-0.10 to 0.09 |
97.5 |
||
Set 2 |
Qt & Qt-1 |
AR2 |
0.996 |
134.7 |
0.992 |
108.2 |
0.997 |
121.9 |
-0.09 to 0.10 |
97.5 |
GANN2 |
0.997 |
106.0 |
0.992 |
104.6 |
0.997 |
105.3 |
-0.08 to 0.09 |
98.3 |
||
Set 3 |
Qt, |
AR3 |
0.996 |
134.6 |
0.992 |
107.1 |
0.997 |
121.3 |
-0.09 to 0.09 |
97.5 |
GANN3 |
0.998 |
87.8 |
0.992 |
100.4 |
0.998 |
94.3 |
-0.06 to 0.10 |
98.3 |
||
Set 4 |
Qt ,Qt-1, Qt-2 & Qt-3 |
AR4 |
0.996 |
134.9 |
0.993 |
99.9 |
0.997 |
118.5 |
-0.09 to 0.07 |
97.9 |
GANN4 |
0.999 |
65.7 |
0.993 |
96.9 |
0.999 |
83.1 |
-0.07 to 0.05 |
99.2 |
||
RESULTS AND DISCUSSION
The performance of the developed models is evaluated for forecasting 1-day-ahead flows in the Kosi River at Baltara in India for the monsoon period (June-Oct).Table 2 summarizes the performance of the developed models. To facilitate comparison, these models are bracketed into four sets. The following section illustrates the performance and sensitivity of the developed models.
The models of Set 1, i.e., AR1 and GANN1, consider only one input, the current-day flow, Qt, to predict next day flow. The objective is to investigate effectiveness of these simple models. ANN (1,3,1) is found suitable for application to GANN1 by a GA scheme comprising population size of 50, crossover probability of 0.85 and mutation probability of 0.002 as it yielded the minimum value of RMSE between the observed and the predicted values for the derivation as well as the verification dataset. Its prediction accuracy for the whole dataset is as high as 97.5% for the Kosi, while the corresponding accuracy by AR1 is 96.3%. In addition, GANN1 shows better CC value of 0.995 and the lesser RMSE value of 151.3 m3/s for the whole dataset. Another performance indicator, DR, which is commonly used as an error measure between the observed and the predicted time series, also seems superior for the GANN1 with value of -0.10 to 0.09 for the whole dataset, suggesting that GANN1 is unbiased, neither under- nor over-predicting. On comparison, prediction by AR1 is skewed significantly toward the negative side. Another input, Qt-1, is added for the models in Set 2. As evident from Table 2, performance of both models improves; the more significant improvement is seen in the performance of GANN model, with its RMSE reducing to 105.3 m3/s, for the whole dataset. The other performance indices, CC, DR and %Accuracy also improve. An additional input, Qt-2,is added to the models of Set 3. As can be observed, all models show some improvement for the derivation, verification and the whole datasets,
The time of concentration, as estimated by the Kirpich equation (Kirpich, 1940) comes to be around four days for the Kosi River at Baltara gauge-site, implying that the flood water from the remotest place in its catchment takes as many days to reach the gauge site. With this in mind, models GANN4 and AR4 are constructed with four previous days’ flow as inputs. Thus, GANN4 and AR4 have Qt-3, Qt-2, Qt-1 and Qt as inputs. After trying many combinations of population size, crossover and mutation, a GA scheme of population size of 350, Gaussian crossover fraction of 0.75, Gaussian mutation function with scale and shrink 2 each and reproduction with elite count of 3, finds the network (4,12,1) optimal for GANN4 GANN4. The objective has been, as in the previous cases, the minimization of RMSE between the predicted and the observed flows. Table 2 shows that all models improved slightly. The GANN4 is found to be the most reliable forecasting model in sets for the Kosi with the highest CC of 0.999, the least RMSE of 83.1 m3/s and the highest %Accuracy of 99.2.
Figure 3 shows percentage of the predicted flows for the whole dataset falling into different discrepancy brackets by the best performing models. The objective is to show how the predicted values compare against the observed values. This figure reaffirms that the GANN4 model predicts river flow better than AR models as the deviation between the predicted and observed discharges is minimum.
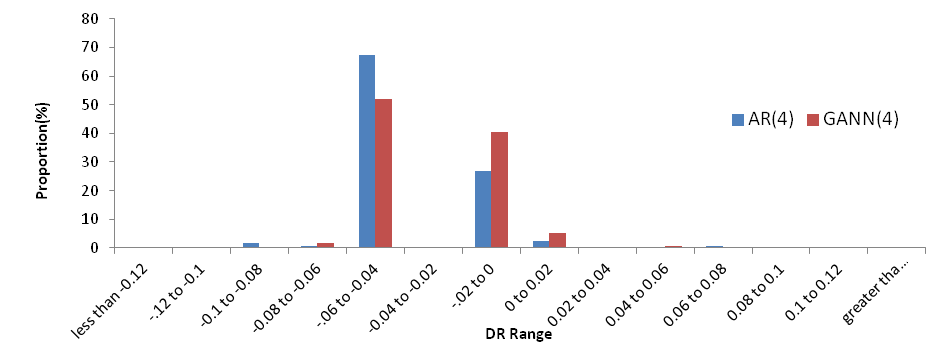
Figure 3: Obs. and pred. flows by the best models (GANN4, verification dataset)
GANN models are seen to be efficient in flood forecasting. However, it should be understood that the present study used daily flow data only for 5 years which included limited number of high flows. This length of data may not be representative of the complexity of the large river systems like that of the Kosi and the models may have overfitted the data. If so, these models would give unsatisfactory forecast for a new and unknown data. Moreover, the developed models are location and period specific, i.e., developed for the Kosi at Baltara gauge-site for the monsoon period. Hence, the models may be sensitive and have significant phase problems if made to forecast flows for the other periods, as the causes of floods may be different in different time periods. During June-Sept, for example, intense monsoon rainfall causes floods in these rivers, while during Oct-Dec, retreating-monsoon and during Jan-May, Himalayan glacier-melt influence flows significantly in North Bihar Rivers. Therefore, models should be developed specifically for a given period utilizing data for the same period.
CONCLUSIONS
The traditional methods are not very efficient for forecasting highly nonlinear monsoon flows. Intelligent methods are also not very accurate unless their parameters are optimized. In this study, a coupled model GANN was developed embedding GA and ANN for predicting monsoon river flows of the Kosi River at Baltara in North India. Based on several performance indices, it was concluded that GANN models predict monsoon flows better than AR models, developed for the comparison purpose. The best GANN model developed for the Kosi predicted flows with the highest accuracy of 99.2%, the highest correlation coefficient of 0.999 and the least root mean square error of 83.1% m3/s for the whole dataset. The estimates of the extreme flows by this models are also in good agreement with the observed values. On comparison, AR models either significantly under-predict or over-predict these extreme flows.
REFERENCES
ASCE (Task Committee on Application of Artificial Neural Networks in Hydrology). (2000a). Artificial Neural Networks in Hydrology I: Preliminary Concepts. J. of Hydrau. Engg., 5: 115-123.
ASCE (Task Committee on Application of Artificial Neural Networks in Hydrology). (2000b). Artificial Neural Networks in Hydrology II: Hydrologic Applications. J. of Hydrau. Engg., 5: 123-137.
Deb, K. (2002). Multi-Objective Optimization Using Evolutionary Algorithms. John Wiley and Sons Asia.
fmis (2012). Flood Management Information System. Water Resour. Depart., Patna, India.
Goldberg, D.E. (2001). Genetic Algorithms In: Search, Optimization and Machine Learning. Addison-Wesley, New York.
Jeevaragagam, P. and Simonovic, S.P. (2012). Neural Network Approach to Output Updating for the Physically-Based Model of the Upper Thames River Watershed, Inter. J. of Hydrol. Sc. and Techn., 2(3): 306 – 324.
Jothiprakash, V., Kirty, S. and Tara, M.S. (2011). Prediction of Meteorological Variables Using Artificial Neural Networks, Inter. J. of Hydrolo. Sc. and Techn., 1(3-4): 192 – 206.
Kirpich, Z.P. (1940). Time of concentration in small agricultural watersheds, Civil Engineering, 10(6), 362.
Michalewicz Z (1992). Genetic algorithm + data structures = evolutionary programs. Springer, New York.
Taormina R, Chau KW and Sethi R. (2012). Artificial Neural Network Simulation of Hourly Groundwater Levels in a Coastal Aquifer System of the Venice Lagoon. Eng. Applic. of Artifi. Intel., 25: 1670-1676.
Cancelliere, A and Giuliano. (2002). A neural network approach for deriving irrigation reservoir operating rules. Water Resour. Manag. 16, 71- 88.
Chakraborty, K., Mehrotra, K., Mohan C., K., and Ranka, S. (1992) Forecasting the behaviour of the multivariate time series using neural networks. Neural Networks, 5, 961-970.
Hsu, K., Gupta, H. V. and Sorooshian, S. (1995) Artificial neural network modelling of the rainfall-runoff process. Water Resour Res 31(10), 2517-2530.
Jain, S. K., Das, A. and Srivastava, D. K. (1999) Application of ANN for reservoir inflow prediction and operation. J. Water Resour. Plan. Manag. 125(5), 263-271.
Karunanithi, N., Grenney, W. J., Whitly, D. and Bovee, K. (1994) Neural networks for river flow prediction. J Comput. Civ. Eng. 8(2), 201-220.
Maier, H. R., and Dandy, G. C. (1996) Empirical comparison of various methods for training feed-forward neural networks for salinity forecasting. Water Resour. Res. 35(8), 2591-2596.
Minns, A. W. and Hall, M. J. (1996) Artificial neural networks as rainfall runoff models. Hydrological Sci. J. 41(3), 399-418.
Nagesh, D., Kumar, L. U. and Peterson, M. R. (2002) Multisite desegregation of monthly to daily stream flow. Water Resour. Res. 36(7), 1823-1833.
Ozgar, K. (2004) River flow modelling using artificial neural networks. J. of Hydro. Engineering 9(1), 60-63.
Randall, W. A. and Tagliarini, G. A. (2002) Using feed forward Neural networks to model the effect of precipitation on water levels of the Northeast Cape Fear River. Proceedings IEEE Southeast conf, pp 338-345.
Shukla, M. B., Kok, R. P., Clark, S. O. G. and Lacroix, R. (1996) Use of artificial neural network in transient drainage design. Trans ASAE, 39(1), 119-124.
Smith J. and Eli RN (1995) Neural-network models of rainfall-runoff process. J. Water Resour. Plng. and Mgmt, 121(6): 499-508.
Thirumalaiah, K. and Deo, M. C. (1998) River flood level forecasting using artificial neural networks. J. of Hydro. Engineering 3(1): 26-32.
Trajkovic, S, Todorovic, B. and Stankovic, M. (2003) Forecasting of reference evapotranspiration by artificial neural networks. J Irrig. Drain. Eng. 129(6), 454-457.
Yang, C. C., Prasher, S. O. and Lacroix, R. (1996) Application of artificial neural network to land drainage engineering. Trans. ASAE 39(2), 525-533.
| *Copy right reserved © 2010 BBrains Development Society. Manthan Publishing House at Patna |
