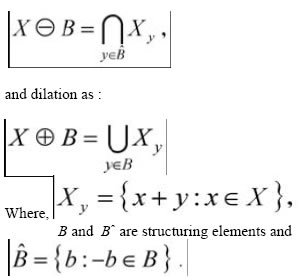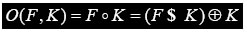Neha Gautam, Rahul Gaurav

Neha Gautam, Rahul Gaurav

Department of Information Technology, Kuvempu University, India,

Department of Electronics Engineering, Isik University, Turkey

Abstract

Mathematical Morphology technique was first proposed in France in sixties for providing a very coherent theoretical framework for image processing and analysis.
This theory was receiving very little attention that time but nowadays, is becoming an object of research in many laboratories and international conferences. Recently, this tool has emerged as an important research topic as the image analysis field is expanding rapidly. Eventually, its impact has been evident by the specialist in the area of both spatial information theory and theories involved in digital image processing and analysis and others related to Mathematical Sciences as well.
The methodology used in this paper is likely to be useful for strategic analysis based on the mathematical theories of sets and topological notions, its principle lies in studying the morphological properties (shape, size, orientation etc.) of the objects through non-linear transformations associated with a reference object (the structuring element).
This paper presents a set theoretical approach and elucidates the basic concepts of the mathematical morphology in a rather general framework as the classical tool of analysis and segmentation of images. We will also identify some future research directions for mathematical morphology.

Mathematical Morphology: Image Analysis Perspective

et theory, topology, lattice algebra, random functions, stochastic geometry, etc. It helps us to perform automated measurements on image data. Thus, it involves set theoretic method of image analysis providing a quantitative description of geometric structures. It is most commonly applied to digital images, but it can also be employed on surface, surface meshes, graphs, solids and many other spatial structures. It characterizes various topological and geometric continuous-space concepts such as shape, size, convexity, connectivity and geodesic distance on continuous and discrete spaces. It is based on shapes in the images not the pixel intensities that are viewed as a general image-processing framework. Generally we use it before and after image segmentation (except the case of watershed segmentation). Two fundamental morphological operations – erosion (shrinking) and dilation (expansion) are based on Minkowski operations.

There are two different types of notations for these operations: Serra/Matheron notation and Haralick/Sternberg notation. In this paper, Haralick/Sternberg notation is used which is the more often used one in case of practical applications.

In this notation erosion is defined as follows (Eq. 1)


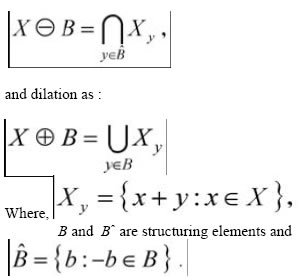
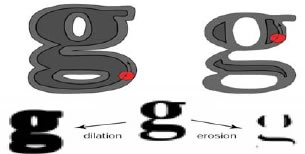
Fig 1 Dilation and erosion by a structuring element

There are two types of composites relations; one is called morphological opening and the other as morphological closing. The main aim of opening is to remove unnecessary structures in the image like noise. Binary opening removes the small regions that are smaller than the structuring element. It is defined as erosion followed by dilation and is given as an image F opened by a SE K:



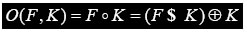
In the fig 1, it has been shown how morphological opening can remove a strip of land projecting into a body of water (capes), a relatively narrow strip of land (with water on both sides) connecting two larger land areas (isthmus) and island which are smaller than the structuring elements
In the fig 2, filling of an arm of a sea or ocean partly enclosed by land (gulfs), channels and lakes small than the structuring elements has been explained.








It is a powerful tool for solving various image relatequeries and also for such operations, which are difficult to expressed by other tools, MM help us express such tougher operations in a rather easier way, such as the boundary extraction example. This approach is often used to post-process “threshold” images then performs some MM operations (like clean up noise, fill in holes) and as a result providing a nice segmented region

The need for morphology has been evident in various fields of science and engineering as well which has been substantiated in recent years like the one in which
it acts as one of the best methods to eliminate weak network lines so that there is an emergence of strongly connected sub-networks in such way that one can predict the behavior of the network. With the help of mathematical morphology, power network images are being decimated for analytical view. It gives a quick view of the strong sub-networks in the power system. In the recent years, morphology has shown its need to the researchers in the realization of several topics like image enhancement, image segmentation, image
restoration edge detection, texture analysis, feature generation, skeletonization, shape analysis, image compression, component analysis, curve filling, general thinning, feature detection and noise reduction. It has shown directions to several researches and development works across the globe by providing an easier method in several image related applications. It
helps in the teeth detection of a gear using subtraction and labeling, in getting the grid identification from Biochip by detecting the size of parts and analyzing its shape (pattern spectrum) using OTSU and entropy threshold. Another important application lies in the detection of runways in satellite airport imagery, which is a multi step algorithmic process that involves White Top-hat Transformation (segmentation tool that extracts respectively dark objects from the uneven background) of the source, image threshold and reconstruction of the detected long features to get the ultimate result. It’s easy-to-use mathematical techniques have helped in the medical field too. In the detection of filarial worms, this tool has been proven to be the most efficient one. In such cases, Black Top-hat Transformation of source is firstly done [fig 5]. Hence the reconstruction after eliminating the short structures of the skeleton gives the final result.

In this paper, the applications and effectiveness of mathematical morphology was presented . the way in which it is beneficial in dealing with many image-related problems, through various cited examples which were brought forth in a lucid manner. We saw the strength and versatility of this technique through the review of previous research works in this domain.
It has been rightly remarked by a famous researcher “though mathematical morphology is a powerful tool for many image analysis, it is not that famous because it is not useful or it is not used so it is not famous, may be because it involves too many mathematical theory!” but we saw the aspect in which it can be dealt with several image queries
Hence, we conclude on this note of discussion that in spite of not gaining ample recognition .Mathematical Science, Geographic Information Sciences and image Science evidenced the efficiency of morphology and the time has come to prove its enduringness to the critics .
The crux of the matter is that we can await some more precise results in the world of images in the near future where the differences between the morphological and non-morphological operations will be well known to us

Acknowledgement

The authors would like to pay their gratitude to Mr Bibhuti Bikramaditya for his commendable support and valuable suggestions during the preparation of this paper.

References

1. Rahul Gaurav, " A Mathematical Morphological Perspective in world of images", seminar on Spatial Information Retrieval, Analysis, Reasoning and Modelling 18th-20 th March 2009. ISI-DRTC, Bangalore, India
2.Hugues Talbot, “Image Analysis and Processing Mathematical Morphology" ESIEE-ECP2006
3.Wyne Hsu, Mong Li Lee, Ji Zhang, “Image Mining: Trends and devlopments",Journal of inteligent Information Systems Volume 19, Issue 1 (July 2002).
4.William Green, “Edge Detection Tutorial.” Internet: http://www.pages.drexcel.edu/~weg22/edge.
html, 2002. 3. M. Kowalczyk , P. Koza, P. Kupidura , J. Marciniak, “APPLICATION OFMATHEMATICAL MORPHOLOGY OPERATIONS FOR SIMPLIFICATION AND IMPROVEMENT OF CORRELATION OF IMAGES IN CLOSE-RANGE PHOTOGRAMMETRY”, The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Vol. XXXVII. Part B5. Beijing 2008 .
5.Adrien Bousseau, “Mathematical Morphology a non exhaustive overview”, pages 2 -14.
6. Radhakrishnan, B. D. S.Sagar, and B. Venkatesh,” Morphological Image Analysis of Transmission Systems”IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 20, NO. 1, JANUARY 2005
7.Pierre Soille, Morphological Image Analysis. Springer-Verlag, 2003.
8.Rafael C. Gonzalez, Richard E Woods. Digital Image Processing. Prentice Hall . second edition,2002.
9.Milan Sonka et. al. Image Processing, Analysis and Machine Vision. PWS publishing, second edition ,1999.
10.Edge Detection using mathematical morphology ,Neil scott, RESEARCH CENTER FOR INTEGRATED MICROSYSTEMS-UNIVERSITY OFWINDSOR, June 15th, 2007.
11.LIXU GU, SEMINAR SERIES ON ADVANCED MEDICAL IMAGE PROCESSING LIXU GU, Robarts Research Institute London, Ontario, Canada, September 13, 2002.
12.L. Najman, Using Mathematical Morphology for Document Skew Estimation, Laboratoire A2SI, Groupie ESIEE cit'e Descartes,BP99.
13.. Mel F. Goodchild, University of California, Santa Barbara, GEOGRAPHICAL INFORMATION SCIENCE FIFTEEN YEARS LATER, page 2-4.
14. Center of Mathematical Morphology (http://cmm.ensmp.fr/index_eng.html) at Ecole des Mines de Paris.
15. Morphology Digest (http://www.cwi.nl/projects/morphology) edited by Henk Heijmans, center for Mathematical and Computer Science, Amsterdam, The Netherlands “Image analysis and mathematical morphology” by J. Serra (call# TA1632.S47 v.2 1988) .
16“Image analysis and mathematical morphology” by J. Serra (call# TA1632.S47 v.2 1988).
17.Ole Christian Eidheim,” Introduction to Mathematical Morphology”, Department of Computer and Information Science, NTNU.
18. Shivprakash Iyer, Sunil K. Sinha J., 2005. Automated condition assessment of buried sewer pipes based on digital imaging techniques. Indian Institute of Science, Sep.–Oct., 85, 235–252.

Corresponding Author:
Email: #neha.niitp@gmail.com
*rahulgaurav.kist@yahoo.com