Abstract

An Analytical expression for molecular association on the phase coexistence properties of fluid with one or two direction attractive centre is discussed .The basic theory of Rosenfeld for the hard sphere is extended to inhomogeneous fluids on the basis of density function. The density functional approach in the grand canonical ensemble utilized to determine thermo dynamical properties of the inhomogeneous fluids. The theoretical prediction is in good quantitative agreement with the simulation result which is available

INTRODUCTION

The theoretical methods for predicting equilibrium properties of homogeneous non-polar fluids are now well documented; much less understood are the properties of confined associating fluids. The density functional theory is routinely used to investigate the properties of simple inhomogeneous system. For anisotropic association, molecular simulations are often computationally intensive and analytical theories give faithful representation of the local fluid structure1. The interplay between chemical association and in-homogeneity makes the phase behaviour of confined associating fluids interesting but difficult to predict.

2. BASIC THEORY

2 (a) Potential Model
We consider a binary mixture of neutral and associating hard spheres confined between two parallel hard walls. The pair-wise two body potential is given by

u(r12,ω1ω2)= uR((r12) +ΣAΣBu(rAB,ω1ω2), (1)

where r12 is the center to center distance between sphere 1 and 2, ω1 and ω2 represents the orientations of the two spheres, and the double sum applies over all associations sites. The reference potential uR represents hard sphere repulsion is given by
uR(r12)=8, r12 < (s1 + s2) / 2 =0, r12 > (s1+ s2) / 2, (2)
where s1 is the hard sphere diameter for component i. The association potential uAB represents the potential between a bonding site A on a spherical particle and a bonding site B from a different sphere with the condition when the attraction sites A and B on molecules 1, 2 prevents molecules 3 from coming close enough to form bond with either site A or B. The association potential is
uAB(r12,&omega1ω2)=-ε,r12< rc=0, otherwise
2 (b) Theory
Let us consider a model in which molecules are assumed to have one bonding site that allows for the formation of dimmers in the system, short ranged, highly anisotropic attractions are obvious choices as models for chemical bonding in the frame work of density functional theory (DFT). The grand free energy can be written as a function of .μi Ω(ρi(r))=(F(ρi(r))+3εi=1∫drpi(r)[φ(r)-μi] (4)
In an open system, the minimization of this grand potential at constant chemical potential , and absolute temperature T, determines the properties of the equilibrium states satisfies

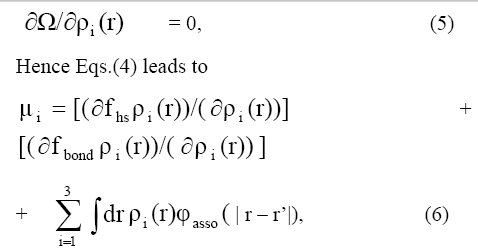
where fhs(ρ(r)) denotes the local free energy density of a uniform hard-sphere density of a uniform hard-sphere fluid,fbond(ρi(r)) corresponds to the local change in the free energy, is the attractive part of the isotropic association potential between particles and i=1,2,3. The Helmholtz free energy φasso(|r-r|) is expressed as contribution from an ideal gas terms and an excess term due to intermolecular interactions

Hence Eqs.(4) leads to

The ideal gas contribution is given by the exact expression

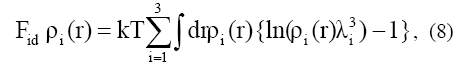
where λ1=(h/(2pmkT)½) represents the thermal wavelength. Here in a typical perturbation approach, the Helmholtz free energy for a system of inhomogeneous associating hard-sphere consists of hard sphere reference system and perturbation.

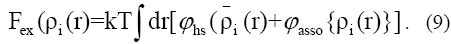
Once we have an expression for the intrinsic Helmholtz free energy, solution to Eq.(5) gives the equilibrium density profiles and subsequently, thermodynamics properties. Equating the chemical potential of each component to that of the bulk fluid mixture of density with which it is in equilibrium, the density distribution for the ioi?th component can be expressed as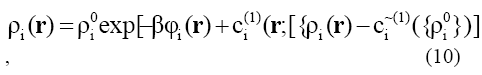

where